堆-二项堆
堆-二项堆
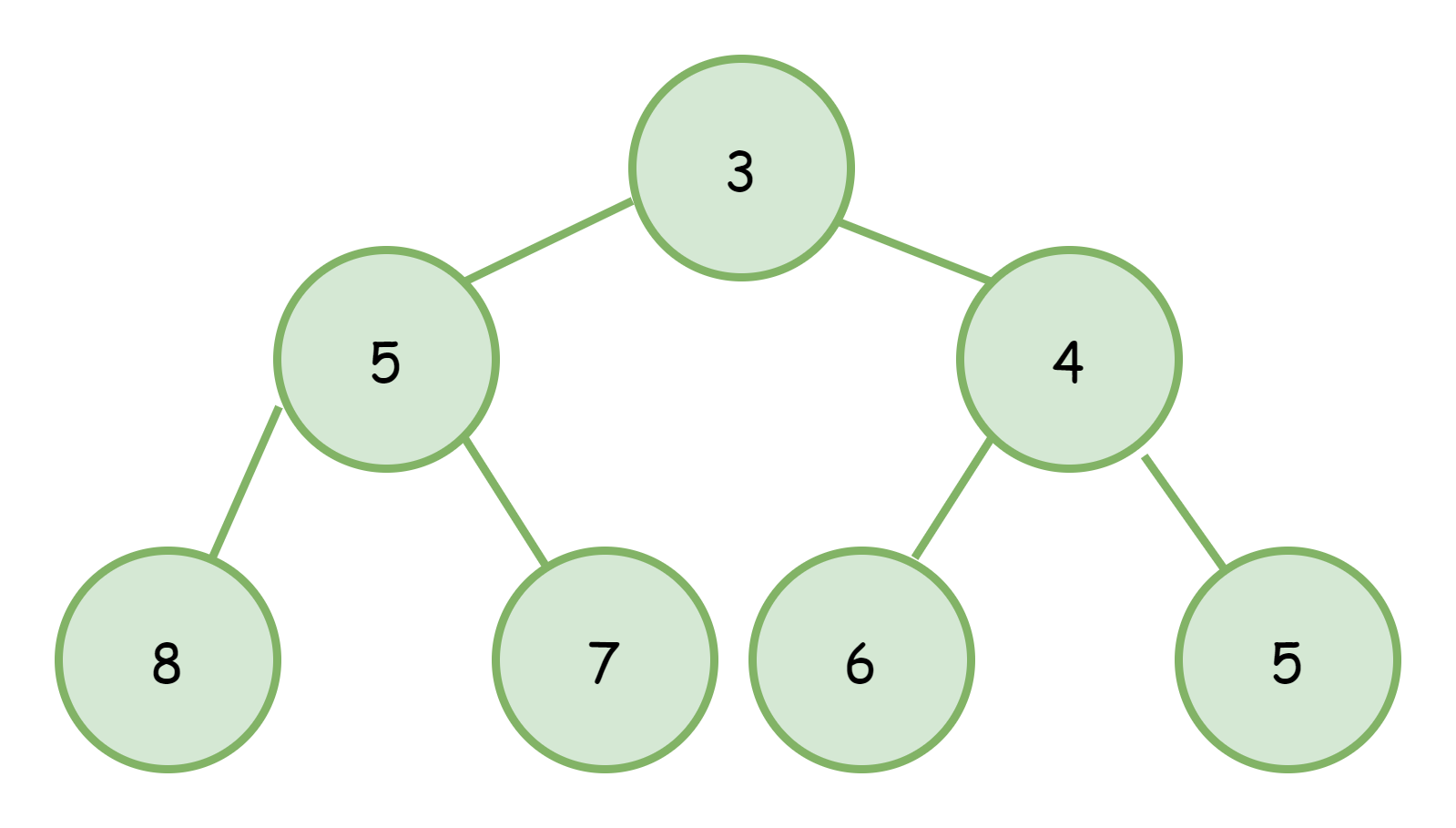
堆是一种特殊的数据结构,它的特点在于可以在O(1)的时间内找到堆内的最大值或最小值。它一般有两种类型,大顶堆或小顶堆。大顶堆是最大值在堆顶,子节点均小于根节点;小顶堆是最小值在堆顶,子节点均大于根节,同时堆也是优先队列比较常见的实现种类。堆只是这类数据结构的统称,并非特指某种具体实现,一般来说它支持以下几种操作,
type Heap[T any] interface {
// 添加若干元素到堆中
Push(e ...T)
// 查看堆顶元素
Peek() (T, bool)
// 返回堆顶元素,并将其从堆中删除
Pop() (T, bool)
// 替换指定元素
Fix(i int, k T)
// 删除指定元素
Remove(i int)
// 两个堆合并
Merge(heap Heap[T])
}
上面这些操作在其它文章可能叫法不一样,但大致的作用都是类似的,也可能有更多的拓展。
今天要讲的就是堆里面最简单的实现,二项堆,或者叫二叉堆,其英文名为BinaryHeap,下面统称为二项堆。二叉堆在表现上通常是一个近似完全二叉树的树,如下图
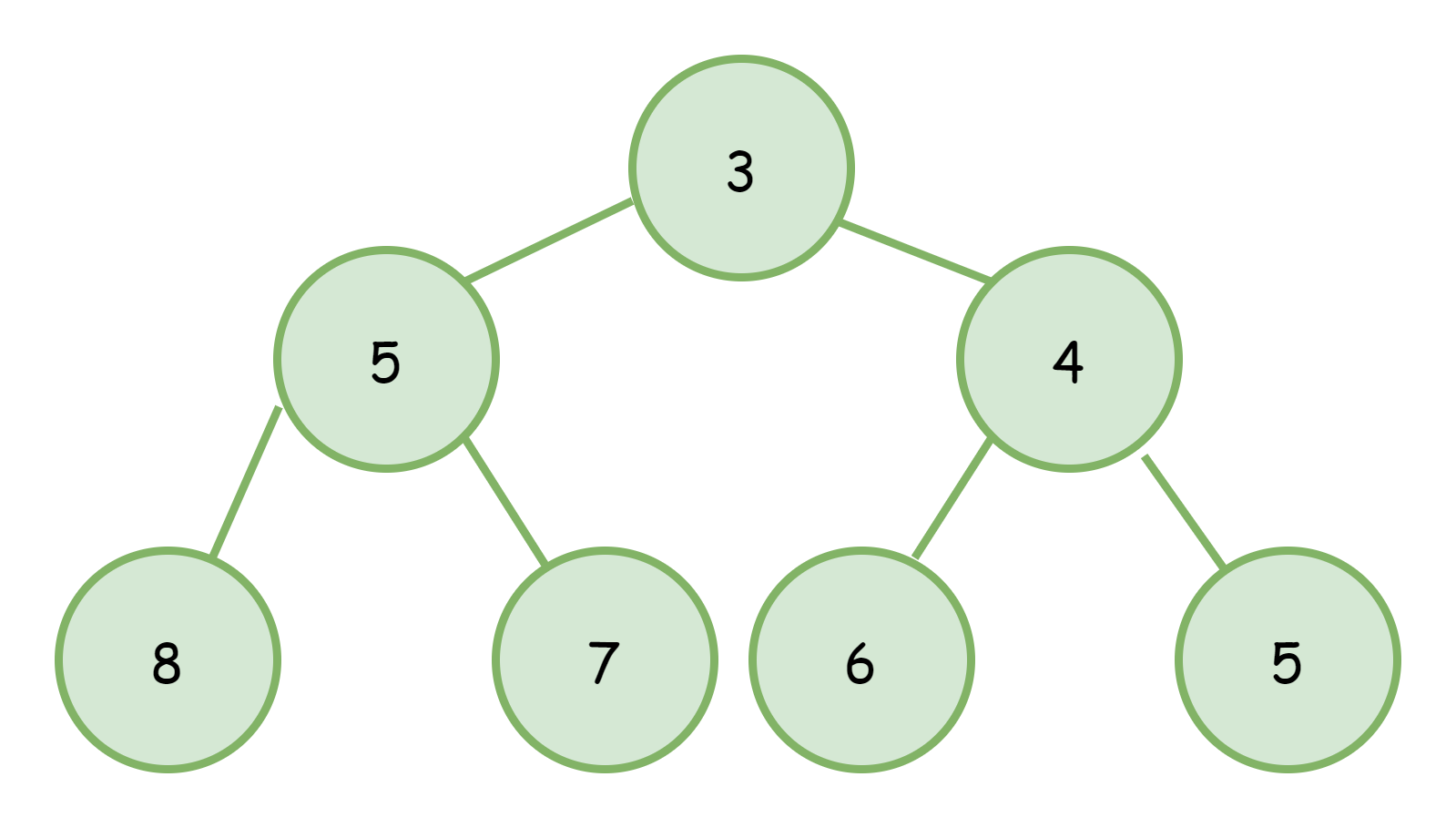
对于二项堆而言,它的关键操作在于元素的上浮和下沉,这个过程会频繁的遍历整个树,所以一般二项堆不会采用树节点的方式实现,而是使用数组的形式。将上图的二叉树转换成数组后就如下图所示:

对于堆每一个节点,其在数组中的下标映射为:
- 父节点:
(i-1)/2 - 左子节点:
i*2+1 - 右子节点:
i*2+2
这种规则很好理解,下面演示上浮和下沉操作,默认为小顶堆。
上浮
在前面的基础之上,向堆中添加了一个新元素,我们将其添加到数组的末尾,如下图

然后让其不断的与它的父节点进行比较,如果小于父节点,就进行交换,否则就停止交换。对于2而言,它的父节点位于下标(7-1)/2=3处,也就是元素8,显然它是小于8的,于是它两交换位置。

然后再与其父节点5进行比较,小于5,则交换位置,然后再与父节点3进行比较,小于3,于是再次交换,最终整个堆就如下图所示:

此时2就是堆顶元素,它也的确是最小的那一个元素,于是堆调整完毕,这个过程也就称之为上浮。整个过程只是在不断的与它的父节点进行比较,总比较次数为3,同时这也是树的高度,对于一个含有n个数量的堆来说,添加一个新元素的时间复杂度为O(logn)。代码实现如下
func (heap *BinaryHeap[T]) up(i int) {
if i < 0 || i >= heap.list.Size() {
return
}
// parent = index / 2 - 1
for pi := (i - 1) >> 1; i > 0; pi = (i - 1) >> 1 {
v, _ := heap.list.Get(i)
pv, _ := heap.list.Get(pi)
if heap.cmp(v, pv) >= containers.EqualTo {
break
}
lists.Swap[T](heap.list, i, pi)
i = pi
}
}
下沉
对于堆顶元素而言,如果要将其从堆中删除,首先将其与最后一个元素交换位置,然后再移除尾部元素。如下图所示

然后此时堆顶元素不断与其子节点进行比较,如果比子字节大就交换位置,每一次交换时,优先交换两个子节点中更小的那一个。比如8的子节点是4,和5,那么将8与4进行交换。

再继续与子节点进行比较然后交换,最终如下图所示

此时堆再次调整完毕,堆顶元素仍然是最小值。整个过程只是在不断的与子节点进行比较交换,下沉操作的时间复杂度也为O(logn)。代码实现如下
func (heap *BinaryHeap[T]) down(i int) {
if i < 0 || i >= heap.list.Size() {
return
}
size := heap.list.Size()
// left_son = index * 2 + 1
// right_son = left_son + 1
for si := i<<1 + 1; si < size; si = i<<1 + 1 {
ri := si + 1
sv, _ := heap.list.Get(si)
rv, _ := heap.list.Get(ri)
lv, li := sv, si
// check if right is less than left
if ri < size && heap.cmp(sv, rv) == containers.GreaterThan {
lv = rv
li = ri
}
// check if iv is less than lv
iv, _ := heap.list.Get(i)
if heap.cmp(iv, lv) <= containers.EqualTo {
break
}
lists.Swap[T](heap.list, i, li)
i = li
}
}
构建
对于构建二项堆而言,一个简单的做法是将其视为一个空的堆,然后不断的对每一个末尾的元素执行上浮操作,那么它的时间复杂度就是O(nlogn)。
有一种办法可以做到O(n)的时间复杂度,它的思路是:首先将给定的输入序列按照二叉树的规则在分布在数组当中,自底向上从最后一个父节点开始,每一个父节点就代表着一个子树,对这个子树的根节点执行下沉操作,这样一直操作到整个二项堆的根节点,由于所有局部的子树都已经完成堆化了,对于这个整体根节点的下沉操作也最多只需要比较O(h)次,h是整个树的高度,可以证明这个过程的时间复杂度为O(n),详细的证明过程在wiki中可以查阅,而二项堆的合并过程也与构建的过程大同小异。代码实现如下
func (heap *BinaryHeap[T]) Push(es ...T) {
if len(es) == 1 {
heap.list.Add(es[0])
heap.up(heap.Size() - 1)
} else {
// push one then up one that is the normal method which will run in O(nlogn) time
// but another faster method as follows that reference https://en.wikipedia.org/wiki/Binary_heap#Building_a_heap
heap.list.Add(es...)
// get the last possible subtree root node position
size := heap.list.Size() / 2
// iterate over all subtree root node bottom up, and execute down operation in per root node
// Assuming that the subtrees of height h have all been binary heapified, then for the subtrees of height h+1,
// adjusting the root node along the branch of the maximum child node requires at most h steps to complete the binary heapification.
// It can be proven that the time complexity of this algorithm is O(n).
for i := size; i >= 0; i-- {
heap.down(i)
}
}
}
总结
| 操作 | 时间复杂度 |
|---|---|
| 构建 | O(n) |
| 查看最小值 | O(1) |
| 插入 | O(log n) |
| 删除 | O(log n) |
| 合并 | O(n) |
二项堆是所有实现中最简单的一个,总体来说难度不大,性能尚可,足够满足基本使用。
提示
有关二项堆的具体实现,可以前往containers/heaps/binary_heap.go进行了解,这是我自己写的常用数据结构的库,支持泛型。
