二叉树的遍历

---

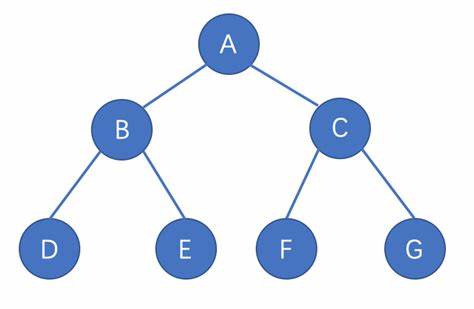
二叉树的遍历分三种

• 前序遍历，中-左-右
• 中序遍历，左-中-右
• 后序遍历，左-右-中

遍历又分递归和迭代版，对于迭代而言就是手动创建栈来模拟递归的调用栈，整体来说都比较简单，只有迭代版的后序遍历需要稍微注意下。

前序遍历

递归版本

func preorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    ans := []int{root.Val}
    ans = append(ans, preorderTraversal(root.Left)...)
    ans = append(ans, preorderTraversal(root.Right)...)
    
    return ans
}

迭代版本

func inorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    var stk []*TreeNode
    var ans []int
    cur := root
    for cur != nil || len(stk) > 0 {
       if cur != nil {
            ans = append(ans, cur.Val)
            stk = append(stk, cur)
            cur = cur.Left
        }else {
            cur = stk[len(stk)-1]
            stk = stk[:len(stk)-1]
            cur = cur.Right
        }
    }
    return ans
}

中序遍历

递归版本

func inorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    lans := inorderTraversal(root.Left)
    lans = append(lans, root.Val)
    rans := inorderTraversal(root.Right)
    return append(lans, rans...)
}

迭代版本

func inorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    var stk []*TreeNode
    var ans []int
    cur := root
    for cur != nil || len(stk) > 0 {
       if cur != nil {
            stk = append(stk, cur)
            cur = cur.Left
        }else {
            cur = stk[len(stk)-1]
            stk = stk[:len(stk)-1]
            ans = append(ans, cur.Val)
            cur = cur.Right
        }
    }
    return ans
}

后序遍历

递归版本

func postorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    ans := postorderTraversal(root.Left)
    ans = append(ans, postorderTraversal(root.Right)...)
    return append(ans, root.Val)
}

迭代版本

func postorderTraversal(root *TreeNode) []int {
	if root == nil {
		return []int{}
	}

	var ans []int
	var stk []*TreeNode
	// 需要一个prev节点来记录上一个出栈的元素
	var prev *TreeNode
	cur := root
	for cur != nil || len(stk) > 0 {
		if cur != nil {
			stk = append(stk, cur)
			cur = cur.Left
		} else {
			// 访问栈顶
			cur = stk[len(stk)-1]
			// 遍历的顺序是左右-中，如果prev == cur.Right
			// 代表已经当前节点的左右节点访问过了，应该出栈了
			if cur.Right != nil && cur.Right != prev {
				cur = cur.Right
			} else {
				ans = append(ans, cur.Val)
				stk = stk[:len(stk)-1]
				prev = cur
				// cur置为nil，走到这里说明左右都已经访问过了，下一次访问栈顶元素
				cur = nil
			}
		}
	}

	return ans
}