队列-双端队列

---

众所周知，队列是一种先进先出（FIFIO）的数据结构，不过它只能一端进，在另一端出，而双端队列对前者进行了拓展，它的两端都能进出。假如，只在一端进，并且只在这一端出，那么这样就变成了后进先出，也就成了栈，因此双端队列其实同时具有队列和栈的性质。

双端队列可以采用链表或数组来实现，本文使用数组的方式来进行讲解。对于双端队列而言，会有两个指针front，tail分别代表的队列的两端。如下图

front指针指向队列的头部元素，而tail则指向队列的尾部，左右端指的是队列的左右端，并非图中数组的左右两端，两者是有很大区别的。

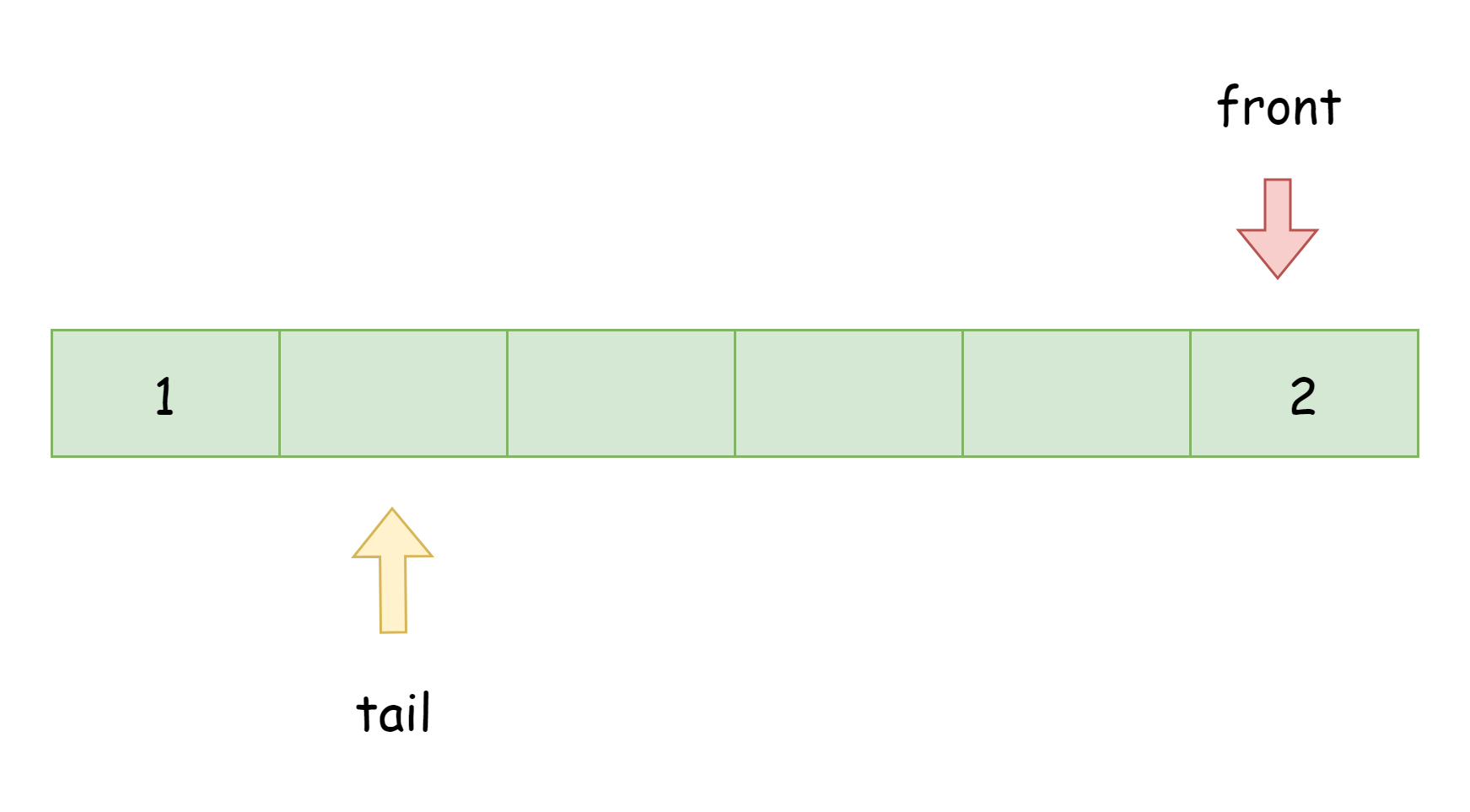
上图中队列内的元素实际为[2, 1]，是左端插入了一个2，右端插入了一个1而产生的结果。通常来说，一个双端队列支持以下操作，如下图

摘自wiki

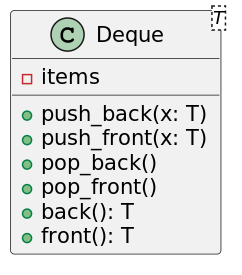
不同语言对这些操作可能会有不同的称呼，但它们的作用都差不多，下面来讲解下双端队列的具体思路。

入队

先来讲讲左边入队，也就是从队列头部添加元素，给定一个如下图所示的空队列，此时front与tail指针重叠，元素数量为0。

从队列左边入队一个元素3，front指针左移，但其本身位于下标0，所以就顺势环形移动到数组末尾，也就是下标5，然后对front所指向的元素赋值3。

此时队列内元素为[3]，假设再从右边入队元素10，从队列右边入队时，先将tail所指向的元素赋值，然后再右移指针tail。所以在入队时，这两个指针其实就是在数组上面环形移动，从数组的一边走到头了，就从另一头继续走，就跟环形链表一样。

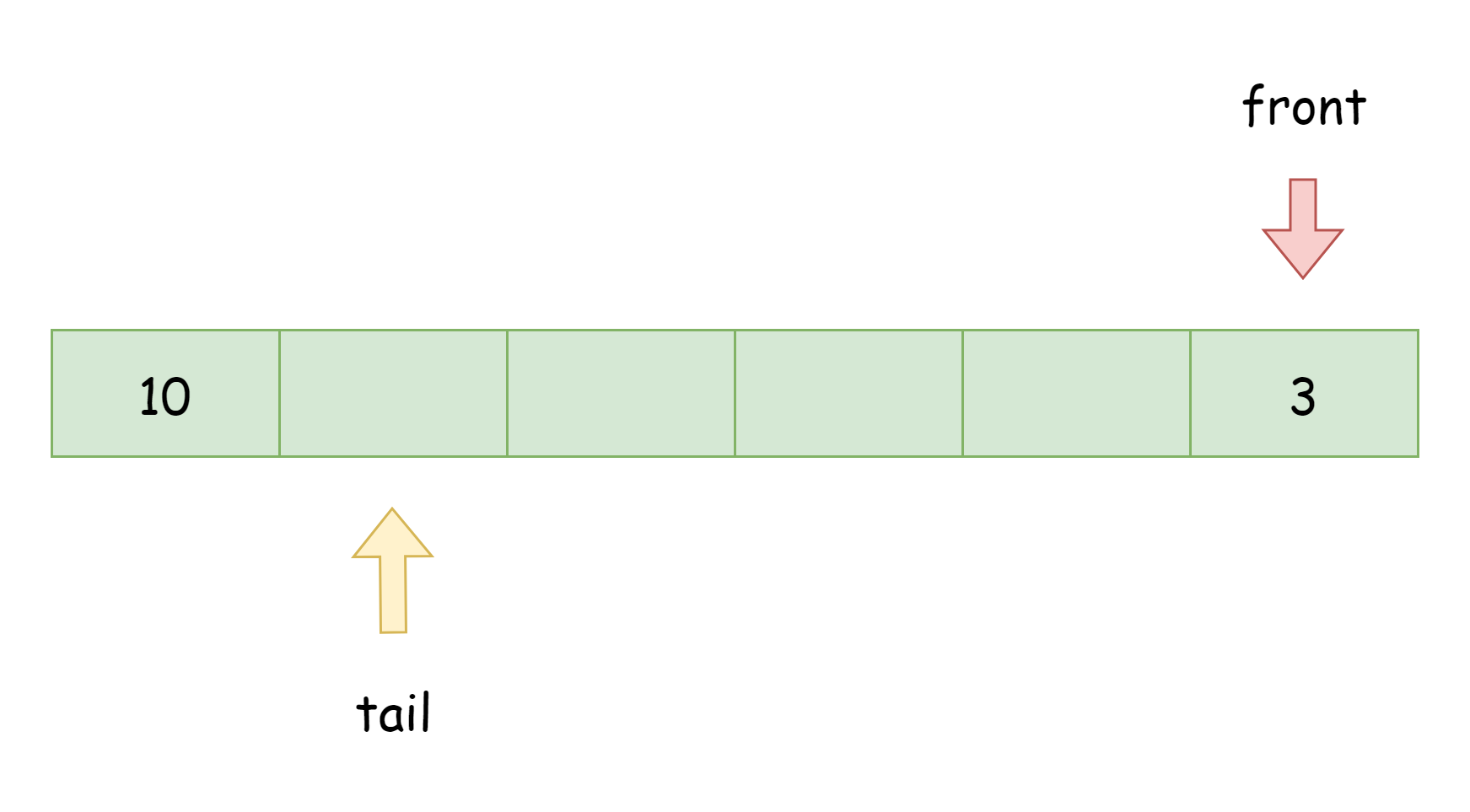
此时队列内的元素为[3, 10]，接下来如果不停在左右端入队元素，那么两个指针此时最终就会相遇，操作如下

1. 左端入队1
2. 右端入队9
3. 左端入队6
4. 右端入队-1

最终结果如图所示，此时队列的元素为[6, 1, 3, 10, 9, -1]，数量为6，队列已经满了，无法再容纳新的元素。

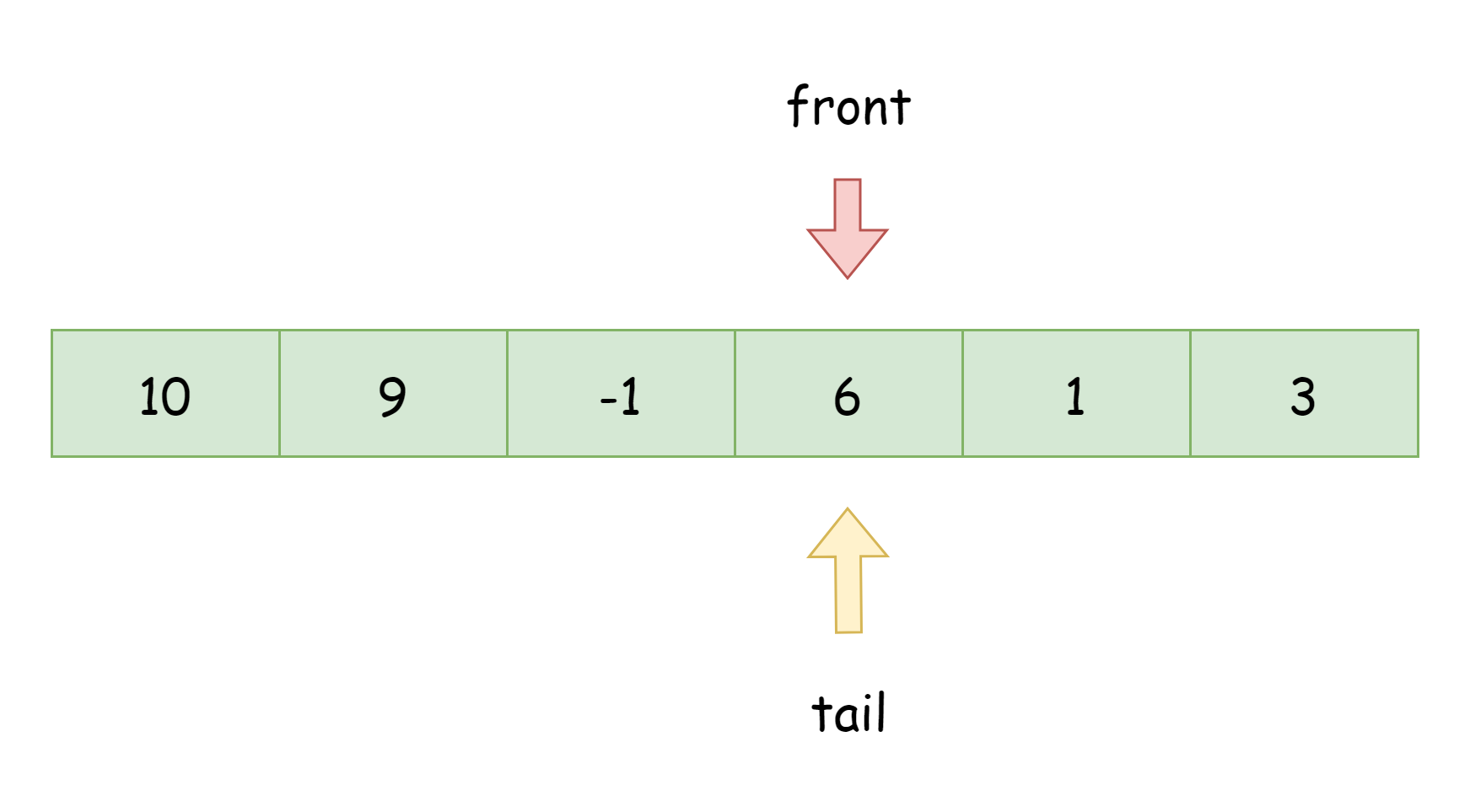
扩容

当双端队列满了以后，如果要继续添加新元素，就需要对其数组进行扩容（有些地方的实现可能不支持扩容），然后让元素重新按照相对位置分布在新的数组上。首先申请一个两倍于当前数组长度的新数组，然后按照原数组中元素的相对位置让它们重新分布在新数组上，对于上图中而言，就是让front指针指向元素（包括自身）的重新右边分布在新数组的右边，然后让左边的元素重新分布在新数组的左边，扩容后的队列数据分布如下图所示，队列左端的元素分布到了数组的右端，队列右端的元素分布在了数组的左端。

在往后的入队操作中，两个指针又会不断靠拢，然后再次扩容，接着又重新分布到新数组的左右两端。

出队

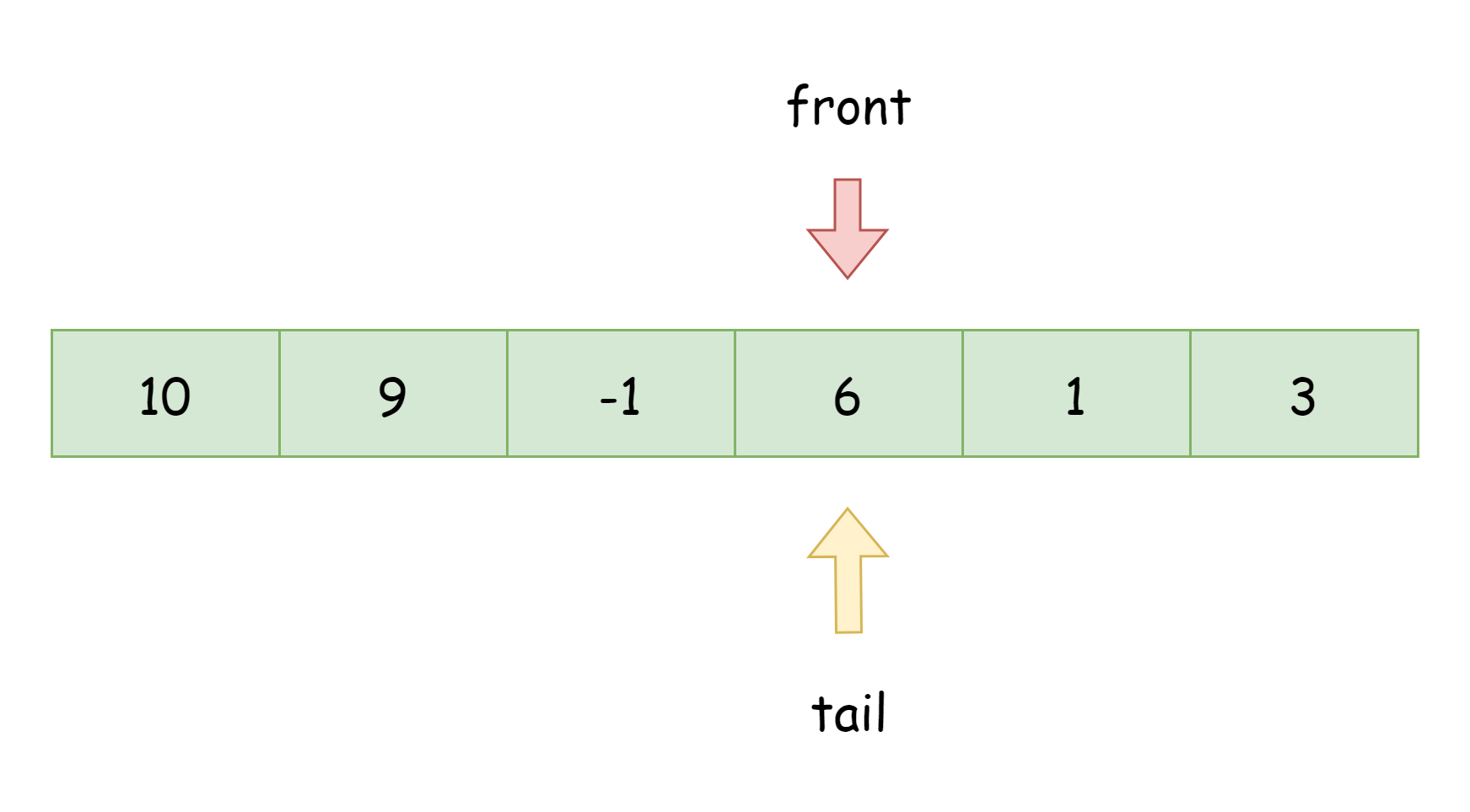
拿上面这一个例子讲解出队，出队其实就是上面的入队的过程反着来。从队列右边出队，只需要将指针tail左移即可，如果有必要也可以将它所指向的元素置0，一般来说不需要。如下图所示，从右边出队元素-1，此时队列内元素为[6, 1, 3, 10, 9]。

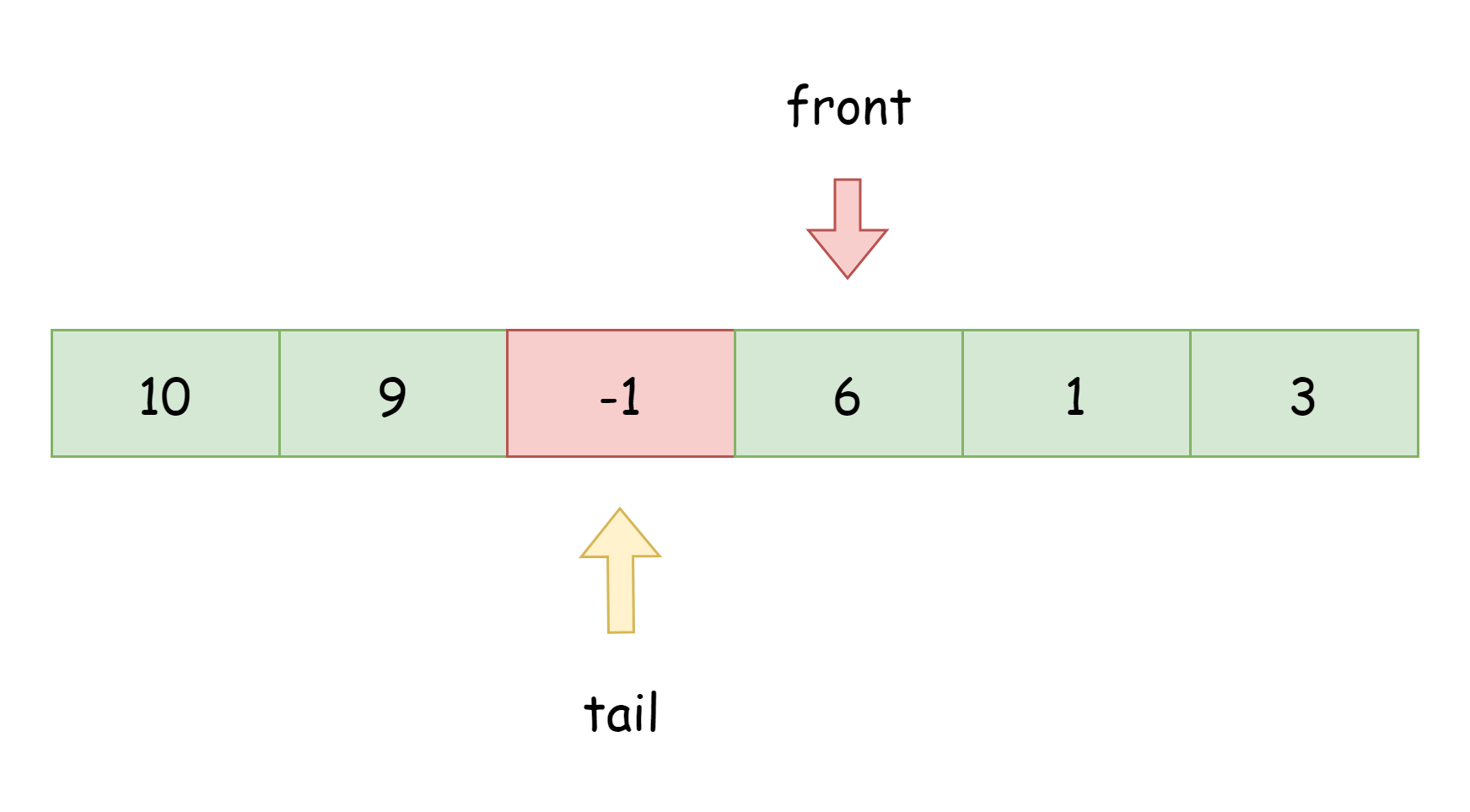
而从左边出队也是一样，只需要将front指针右移。如下图所示，从右边出队元素6，此时队列内元素为[1, 3, 10, 9]。

如此往复，两个指针会分别往数组左右两端移动，直到再次相遇，数组为空。

缩容

当队内元素数量小于数组长度的一半时，可以考虑缩容，这个是可选项，并非所有双端队列都要实现缩容。此时元素都分布在数组的左右两侧，而数组中间有一大堆无用的空间，可以申请一个新的数组，其长度为原来的3/4，也就是原数组缩小了1/4的长度，之所以不直接缩小一半是为了避免往后入队时会频繁的触发扩容操作。沿用之前的例子，假设在缩容前队列如下图所示

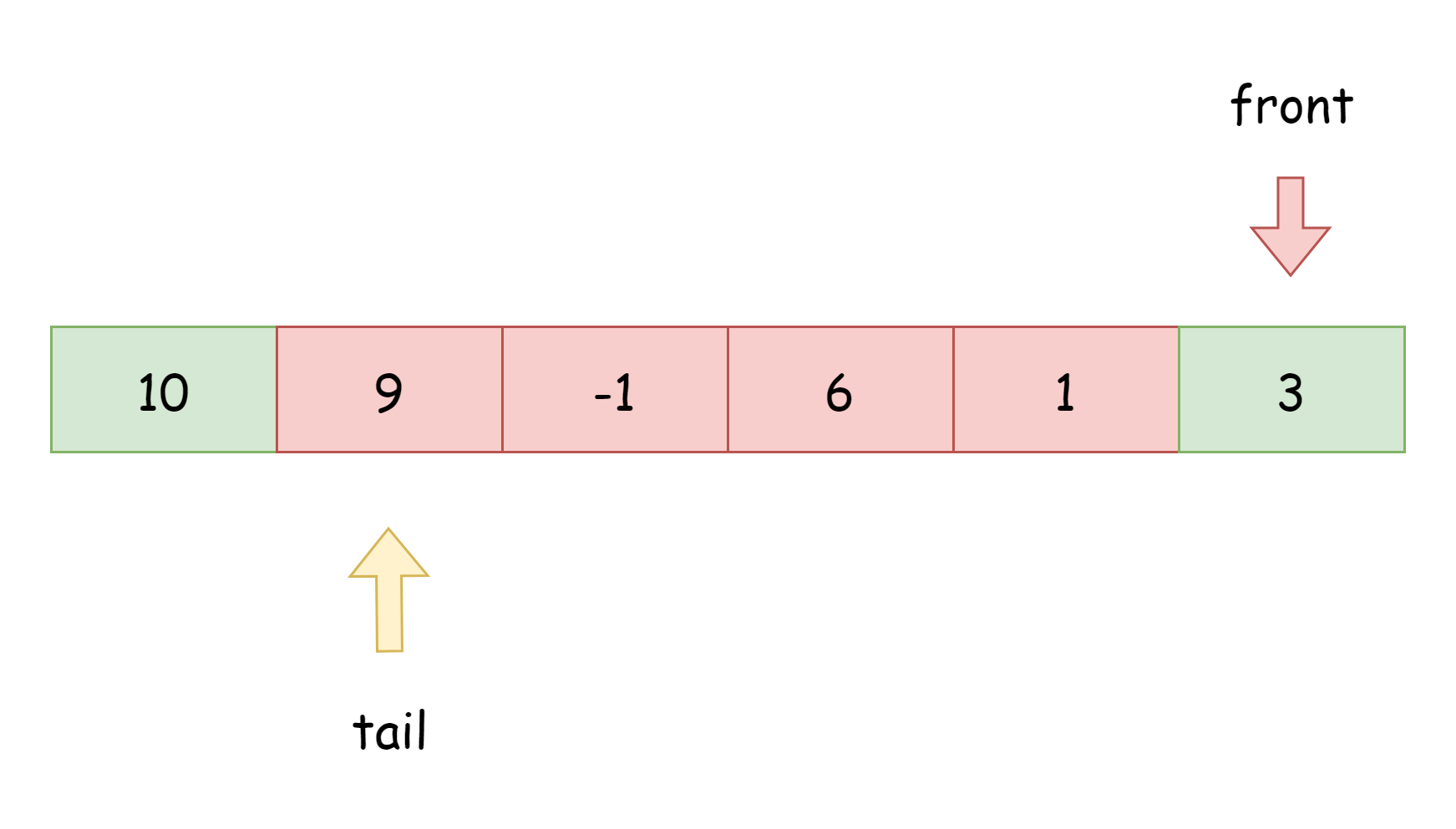
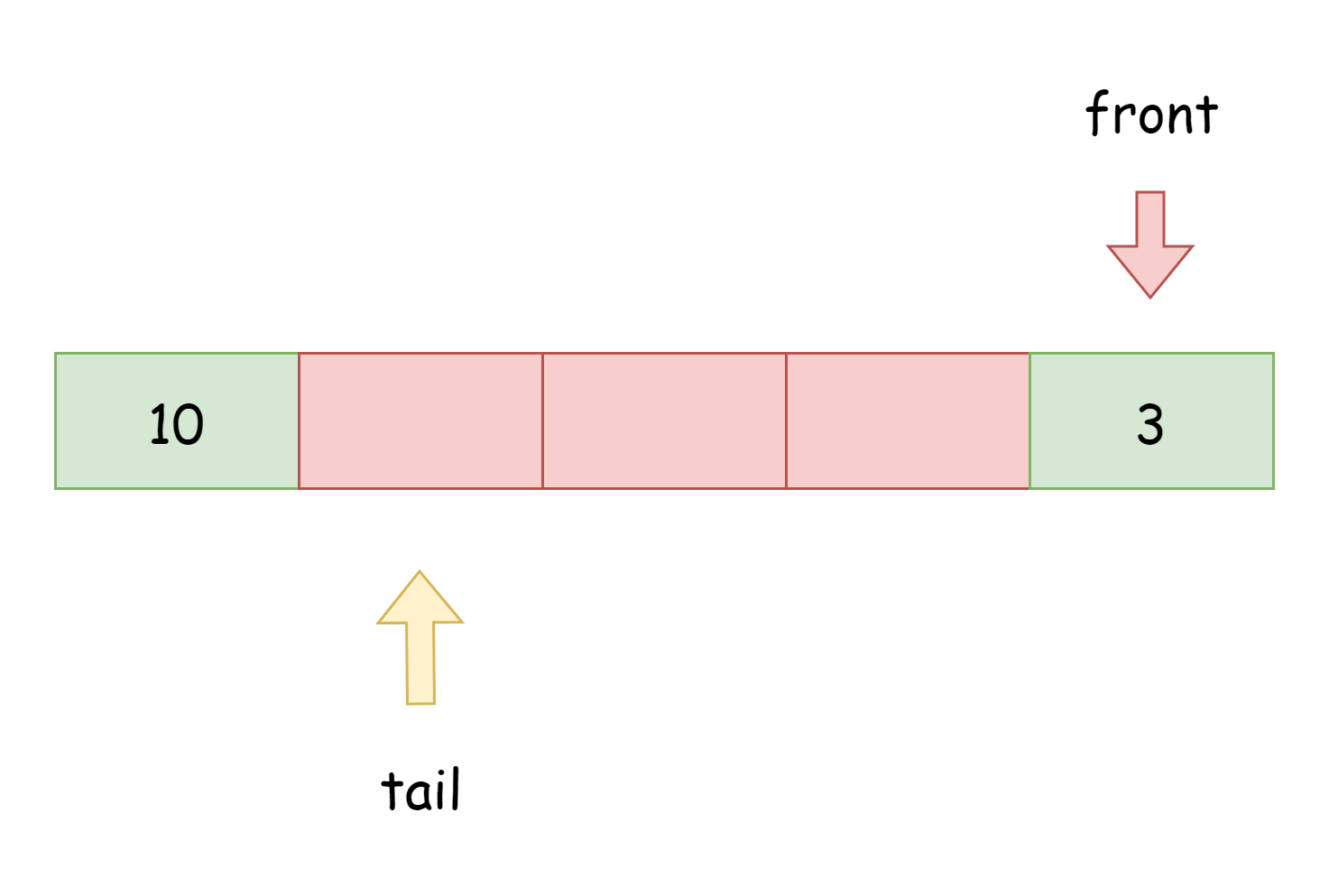
原数组长度为6，缩小1/4就是长度5，然后重新分布元素后，如下图所示

总结

下面是两种不同实现的对比

	动态数组	双向链表
入队	O(n)	O(1)
出队	O(n)	O(1)
随机访问	O(1)	O(n)

对于动态数组实现，它的均摊时间复杂度可以达到O(1)，适合读多写少的场景，而对于双向链表来说，比较时候读少写多的场景。

双端队列的实现代码位于github.com/246859/containers/queues/dequeue.go。