经典排序算法
经典排序算法

冒泡排序
冒泡排序是最简单的一种排序,也是最暴力的排序方法,对于大多数初学者而言,它是很多人接触的第一个排序方法。大致实现思路如下:从下标0开始,不断将两个数字相比较,如果前一个数大于后一个数字,那么就交换位置,直至末尾。外层循环每一轮结束后,就能确定一个值是第i+1大的元素,于是后续的元素就不再去交换,所以内层循环的终止条件是len(slice)-(i+1)。
下面是一个冒泡排序的泛型实现。
func BubbleSort[T any](s []T, less func(a, b T) bool) {
for i := 0; i < len(s); i++ {
for j := 0; j < len(s)-1-i; j++ {
if less(s[j+1], s[j]) {
s[j+1], s[j] = s[j], s[j+1]
}
}
}
}
时间复杂度:O(n^2)
不管情况好坏,它需要交换总共 (n-1)+(n-2)+(n-3)+...+1 次 ,对其进行数列求和为 (n^2-n)/2 ,忽略低阶项则为O(n^2),即便整个切片已经是完全有序的。
空间复杂度:O(1)
算法进行过程中没用到任何的额外空间,所以为O(1)
稳定性:是
两个元素相等时不会进行交换,就不会发生相对位置的改变。看一个例子
1 3 3 0
第一轮冒泡,移动第二个3
1 3 0 3
第二轮冒泡,移动第一个3
1 0 3 3
可以看到相对位置没有发生变化。
性能测试
对其进行基准测试,分别使用100,1000,1w,10w个随机整数进行排序,测试数据如下
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkBubbleSort/100-16 104742 10910 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSort/1000-16 984 1149239 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSort/10000-16 7 158096014 ns/op 1 B/op 0 allocs/op
BenchmarkBubbleSort/100000-16 1 19641943300 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 23.037s
随着数据量的增多,冒泡排序所耗费的时间差不多是在以平方的级别在增长,到了10w级别的时候,要花费整整18秒才能完成排序,值得注意的是整个过程中没有发生任何的内存分配。百万数据量耗时太久了,就懒得测了。
优化
第一个优化点是原版冒泡即便在数据完全有序的情况下依然会去进行比较,所以当一趟循环完后如果发现数据是有序的应该可以直接退出,这是减少外层循环的次数。由于冒泡排序每轮会冒泡一个有序的数据到右边去,所以每轮循环后都会缩小冒泡的范围,假设数据右边已经是有序的了,那么这种操作就可以提前,而不需要等到指定循环次数之后才缩小范围,比如下面这种数据
4,1,3,2,5,6,7,8,9
这个范围的边界实际上就是上一轮循环最后一次发生交换的下标,这是减少了内循环次数。这里提一嘴使用位运算也可以实现数字交换,算是第三个优化点,但仅限于整数类型。优化后的代码如下
func BubbleSortPlus[T any](s []T, less func(a, b T) bool) {
// 记录最后一个交换的下标
end := len(s) - 1
var last int
for i := 0; i < len(s); i++ {
// 记录整个切片是否已经有序
isSorted := true
// 内循环只截至到last
for j := 0; j < end; j++ {
if less(s[j+1], s[j]) {
s[j+1], s[j] = s[j], s[j+1]
isSorted = false
last = j
}
}
end = last
if isSorted {
return
}
}
}
优化只能提高冒泡的平均时间效率,在最差情况下,也就是数据完全逆序/升序的时候,对其进行升序/逆序排序,渐进时间复杂度依旧是O(n^2)。
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkBubbleSort/100-16 104742 10910 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSort/1000-16 984 1149239 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSort/10000-16 7 158096014 ns/op 1 B/op 0 allocs/op
BenchmarkBubbleSort/100000-16 1 19641943300 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSortPlus/100-16 115183 10537 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSortPlus/1000-16 1090 1092803 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSortPlus/10000-16 8 139880100 ns/op 0 B/op 0 allocs/op
BenchmarkBubbleSortPlus/100000-16 1 18904012900 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 51.565s
提升并不是特别明显,因为数据是完全随机的,可能很多生成的数据并没有走到优化点上,这也变相证明了冒泡排序不太适合实际使用。
选择排序
选择排序的思路非常的清晰和容易实现,将数组分为两部分,一部分有序,一部分无序,首先在数组的未排序部分找出其中的最大或最小值,也就是然后将最大值或最小值其与数组的中的第i个元素交换位置。第一个交换的一定是第一大或第一小的元素,第二个就是第二大或第二小的元素,这样一来就确认了有序的部分,如此在未排序的部分循环往复,直到整个数组有序。比如
2 1 4 -1
此时整个数组都是无序的,找出其最小值-1,与第一个元素交换位置
-1 1 4 2
此时只剩[1,4,2]是未排序部分,继续找最小值,得到1,那么它就是第二小的元素,就将其与第二个元素交换位置,由于它本身就在第二个位置上所以没变化。
-1 1 4 2
继续按照这个流程,就能将数据最终变得有序。具体代码实现如下
func SelectSort[T any](s []T, less func(a, b T) bool) {
for i := 0; i < len(s); i++ {
minI := i
for j := i + 1; j < len(s); j++ {
if less(s[j], s[minI]) {
minI = j
}
}
s[i], s[minI] = s[minI], s[i]
}
}
时间复杂度:O(n^2)
不管在什么情况,在选择排序的过程中,它都会在每轮循环后的未排序部分去比较寻找最大值,所以比较次数为(n-1)+(n-2)+(n-3)....+1差不多就是(n2+n)/2,所以其时间复杂度为O(n2)。
空间复杂度:O(1)
排序过程中没有用到任何的额外空间来辅助,所以时间复杂度为O(1)。
稳定性:否
在交换的过程中它们的位置会发生改变,但也不会被调整回来,所以是不稳定的。看一个例子
6 7 6 0 1
第一轮交换第一个6会和0交换位置,就变成了
0 7 6 6 1
本来是在第二个6前面的现在到后面来了,相对位置发生改变了,即便整个数组完成排序后也不会再被调整。
性能测试
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkSelectSort/100-16 109363 10377 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSort/1000-16 1260 939461 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSort/10000-16 13 88333308 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSort/100000-16 1 9028276000 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 13.263s
可以看到的是选择排序在10w数据量时选择排序花费的时间是冒泡的一半左右,这是因为冒泡每轮循环交换的次数比较多,而选择排序每轮循环只交换一次,总体上从时间来说是优于冒泡排序的。
优化
原版选择排序只会在切片的左边构建有序部分,在右边无序的部分去寻找最大或最小值,既然反正都是在无序部分寻找最大/最小值,那就可以在切片左右两边都构建有序区,假设是升序排序,左边是最小,右边是最大,中间就是无序区,这样一来就可以减少差不多一半的比较次数。优化后的代码如下
func SelectSort[T any](s []T, less func(a, b T) bool) {
// 记录左右两边的边界
l, r := 0, len(s)-1
for l < r {
minI, maxI := l, r
for j := l; j <= r; j++ {
if less(s[j], s[minI]) {
minI = j
}
if !less(s[j], s[maxI]) {
maxI = j
}
}
// 没找到就没必要交换
if minI != l {
s[minI], s[l] = s[l], s[minI]
// 如果maxI==l,说明maxI上已经不是原来的那个值了
// 因为l和minI已经交换过了,此时的l就是minI,所以要纠正一下
if l == maxI {
maxI = minI
}
}
if maxI != r {
s[maxI], s[r] = s[r], s[maxI]
}
// 缩小边界
l++
r--
}
}
这样一来,这样一来只需要看一边的比较次数就够了,不严谨的来说就是(n/2-1)+(n/2-2)+(n/2-3)...,最后时间复杂度依旧是O(n^2),不过优化的时间效率上会有所提升。
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkSelectSort/100-16 109363 10377 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSort/1000-16 1260 939461 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSort/10000-16 13 88333308 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSort/100000-16 1 9028276000 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSortPlus/100-16 133096 8826 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSortPlus/1000-16 1447 794633 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSortPlus/10000-16 14 77494886 ns/op 0 B/op 0 allocs/op
BenchmarkSelectSortPlus/100000-16 1 7745074200 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 29.479s
通过数据对比可以看到,在时间效率上大概提升了接近10-20%左右。
插入排序
插入排序也是一种比较简单的排序方法,其基本思路为:假设0 ...i的元素已经有序,使用s[i+1]逆向与前i+1个元素进行逐个比较,如果在比较过程中第j个元素比第i+1个元素小/大,那么将其后移,如此循环往复,直到找到第一个大于/小于s[i+1]下标元素的元素时或者下标为0时,考虑到比s[i]小/大的元素都已经后移了,所以直接s[i]的值覆盖到s[j+1]上。
func InsertSort[T any](s []T, less func(a, b T) bool) {
for i := 1; i < len(s); i++ {
item := s[i]
var j int
for j = i - 1; j >= 0; j-- {
if less(item, s[j]) {
s[j+1] = s[j]
}
}
s[j+1] = item
}
}
时间复杂度:O(n^2)
如果是要升序排列,在最好情况下,要排序的切片已经是完全升序的了,那么只需要进行n-1次比较操作。最坏情况就是完全降序,那么就需要n+(n-1)+(n-2)+......+1次比较,总共就是(n^2+n)/2次。
空间复杂度:O(1)
整个过程中未用到额外的辅助空间
稳定性:是
遇到相等元素时便插入到该元素后面,不会出现跑到它前面的情况。
性能测试
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkInsertSort/100-16 127532 8925 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSort/1000-16 1611 736531 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSort/10000-16 15 71716213 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSort/100000-16 1 7104786500 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 11.312s
优化
插入排序的优化方案很容易想到,假设是升序排列,在确保前n个元素已经是有序的情况下,我们需要去一个个遍历找到第一个小于s[n+1]的元素,既然它是有序的,那就可以使用二分查找来进行操作,然后再移动元素。移动次数没有减少,但比较次数减少了相当的多。优化后的代码如下
func InsertSortPlus[T any](s []T, less func(a, b T) bool) {
for i := 1; i < len(s); i++ {
target := s[i]
// 对有序部分进行二分查找
l, r := 0, i-1
for l <= r {
mid := l + (r-l)/2
if less(target, s[mid]) {
r = mid - 1
} else {
l = mid + 1
}
}
// 移动元素
for j := i - 1; j >= l; j-- {
s[j+1] = s[j]
}
s[l] = target
}
}
看看优化后的性能
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkInsertSort/100-16 127532 8925 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSort/1000-16 1611 736531 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSort/10000-16 15 71716213 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSort/100000-16 1 7104786500 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSortPlus/100-16 399487 2820 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSortPlus/1000-16 7941 187614 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSortPlus/10000-16 79 13721910 ns/op 0 B/op 0 allocs/op
BenchmarkInsertSortPlus/100000-16 1 1290984000 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 28.564s
可以看到使用了二分的插入排序性能整整比原版提升了足足有70-80%左右,这已经是非常巨大的提升了。在最好的情况下,如果切片本身就是全部有序的话,就不需要移动元素,那么就只有查找会消耗时间,这样一来它的时间复杂度可以接近O(nlogn)。在最差的情况,每次都需要移动i-1个元素,那么就是(log(n-1)+n-1)+(log(n-2)+n-2)+(log(n-3)+n-3)....,当n足够大时,logn产生的影响已经微不足道了,虽然没有经过严格的计算,但简单估算下它的时间复杂度依旧不会小于O(n^2)。
不过值得高兴的是,到目前为止总算有一个方法能够有突破O(n^2)的可能性。
希尔排序
希尔排序是插入排序的一个更加高效的优化版本,也称递减增量排序。原版插入排序在数据本身是有序的情况下效率会非常高可以达到O(n),希尔排序的改进思路也是基于此,它在移动和比较时,不再是一个一个移动,而是有了间隔称之为步长。比如下面这个序列
6 2 1 5 8 11 9 0
假设初始步长为3,那么就将数据划分为了三份
6 5 9
2 8 0
1 11
分别对每一份进行插入排序后得到下面的序列,将其拼接再一起,然后再以步长为2进行划分
5 6 9
0 2 8
1 11
5 0 1 6 2 11 9 8
5 1 2 9
0 6 11 8
1 2 5 9
0 6 8 11
此时再拼接回来
1 0 2 6 5 8 9 11
可以发现整体已经接近基本有序的状态了,在这种情况下,步长再减为1就是原版插入排序了,在数据大多数有序的情况下,插入排序的时间复杂度可以接近O(n)。希尔排序的关键就在于,如何选择这个步长序列,步长序列的不同会导致希尔排序的时间复杂度也不同,在某些情况下它可能根本不会起作用。比如下面这个数据,步长的选择是每次折半,会根本发现不会起到任何优化的作用,反而还不如直接进行插入排序,因为无意义的步长划分导致它甚至比原始的插入排序还增加了额外的耗时,要更加的低效率。
2 1 4 3 6 5 8 7
// 步长为4
2 3 7
1 5
4 8
6
// 步长为2
2 4 6 8
1 3 5 7
最简单的步长序列就是每次对半分,这也是希尔本人提出的,这种也最容易实现,当然也最容易出现上面那个问题。
func ShellSort[T any](s []T, less func(a, b T) bool) {
for gap := len(s) >> 1; gap > 0; gap >>= 1 {
for i := gap; i < len(s); i++ {
item := s[i]
j := i - gap
for ; j >= 0; j -= gap {
if !less(item, s[j]) {
break
}
s[j+gap] = s[j]
}
s[j+gap] = item
}
}
}
当最坏情况下,也是上面那个例子的情况下,划分步长没有任何的意义,这就退化成了原始的插入排序,其最差时间复杂度依旧是O(n^2)。为了避免这种情况,就需要仔细斟酌步长序列的选择,最基本的原则就是序列之间的元素得互为质数,如果可以互为因子的话就可能会出现对已经排过序的集合再一次排序这种情况,导致无意义的消耗。
希尔排序首次提出是在上世纪六十年代,现如今已经有了非常多的序列可选,下面介绍比较常见的两个:
- Hibbard序列,最差时间复杂度O(n(3/2))
- Sedgewick序列,最差时间复杂度O(n(4/3)),目前最优序列?
还有其它非常多的序列,前往:Shellsort - Wikipedia了解更多(注意必须是英文维基,中文根本没有这么详细的介绍)。Hibbard实现代码如下,步长序列采用打表的方式记录,不需要每次都来计算步长序列。步长序列本身计算非常简单,难的是求证过程,笔者受限于数学水平,无法在此做出解答。由于序列的增长本身就是次方级别,当增长到数值溢出时的上一个步长就是最大步长了,这样就可以得到一个对于任意长度的切片都适用的步长序列。

var HibbardGaps = []int{
9223372036854775807, 4611686018427387903, 2305843009213693951, 1152921504606846975, 576460752303423487, 288230376151711743, 144115188075855871, 72057594037927935, 36028797018963967, 18014398509481983, 9007199254740991, 4503599627370495, 2251, 799813685247,
1125899906842623, 562949953421311, 281474976710655, 140737488355327, 70368744177663, 35184372088831, 17592186044415, 8796093022207, 4398046511103, 2199023255551, 1099511627775, 549755813887, 274877906943, 137438953471, 68719476735, 34359738367, 17179869183,
8589934591, 4294967295, 2147483647, 1073741823, 536870911, 268435455, 134217727, 67108863, 33554431, 16777215, 8388607, 4194303, 2097151, 1048575, 524287, 262143, 131071, 65535, 32767, 16383, 8191, 4095, 2047, 1023, 511, 255, 127, 63, 31, 15, 7, 3, 1,
}
func ShellSortHibbard[T any](s []T, less func(a, b T) bool) {
if len(s) == 0 {
return
}
n := len(s)
hibbard := HibbardGaps
for i := len(HibbardGaps) - 1; i >= 0; i-- {
// 当步长超过数组长度时候就退出
if HibbardGaps[i] > n {
hibbard = HibbardGaps[i+1:]
break
}
}
for _, gap := range hibbard {
for i := gap; i < len(s); i++ {
item := s[i]
j := i - gap
for ; j >= 0; j -= gap {
if !less(item, s[j]) {
break
}
s[j+gap] = s[j]
}
s[j+gap] = item
}
}
}
对于Sedgewick序列,则有如下两个公式
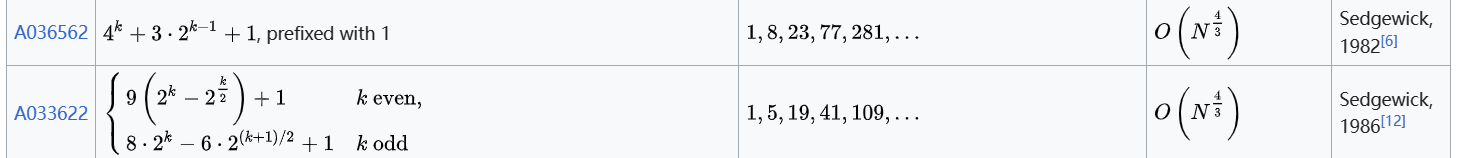
第二个公式要分奇偶情况,这里选择第一个公式,依旧选择打表实现。
var SedgewickGaps = []int{
6917529027641081857, 3458764513820540929, 1729382256910270465, 864691128455135233, 432345564227567617, 216172782113783809, 108086391056891905, 54043195528445953, 27021597764222977, 13510798882111489, 6755399441055745, 3377699720527873, 16888,
49860263937, 844424930131969, 422212465065985, 211106232532993, 105553116266497, 52776558133249, 26388279066625, 13194139533313, 6597069766657, 3298534883329, 1649267441665, 824633720833, 412316860417, 206158430209, 103079215105, 51539607553, 257,
69803777, 12884901889, 6442450945, 4611686021648613377, 1152921506217459713, 288230376957018113, 72057594440581121, 18014398710808577, 4503599728033793, 1125899957174273, 281475001876481, 70368756760577, 17592192335873, 4398049656833, 109951320,
0641, 274878693377, 68719869953, 17180065793, 4295065601, 1073790977, 268460033, 67121153, 16783361, 4197377, 1050113, 262913, 65921, 16577, 4193, 1073, 281, 77, 23, 8, 1,
}
func ShellSortSedgewick[T any](s []T, less func(a, b T) bool) {
if len(s) == 0 {
return
}
n := len(s)
sedgewickGaps := SedgewickGaps
for i := len(SedgewickGaps) - 1; i >= 0; i-- {
if SedgewickGaps[i] > n {
sedgewickGaps = SedgewickGaps[i+1:]
break
}
}
for _, gap := range sedgewickGaps {
for i := gap; i < len(s); i++ {
item := s[i]
j := i - gap
for ; j >= 0; j -= gap {
if !less(item, s[j]) {
break
}
s[j+gap] = s[j]
}
s[j+gap] = item
}
}
}
性能测试
下面是一个简单的性能测试对比
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkShellSort/100-16 555520 2035 ns/op 0 B/op 0 allocs/op
BenchmarkShellSort/1000-16 18080 66212 ns/op 0 B/op 0 allocs/op
BenchmarkShellSort/10000-16 1056 1121350 ns/op 0 B/op 0 allocs/op
BenchmarkShellSort/100000-16 74 15739070 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortHibbard/100-16 674043 1991 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortHibbard/1000-16 18570 62829 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortHibbard/10000-16 1044 1177521 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortHibbard/100000-16 68 17195475 ns/op 2 B/op 0 allocs/op
BenchmarkShellSortSedgewick/100-16 677540 1955 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortSedgewick/1000-16 21933 56625 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortSedgewick/10000-16 1266 928296 ns/op 0 B/op 0 allocs/op
BenchmarkShellSortSedgewick/100000-16 91 12452856 ns/op 1 B/op 0 allocs/op
PASS
ok sorts 126.826s
可以看到的是Sedgewick步长序列在时间效率上有着较为明显的提升,Hibbard则不太明显。
堆排序
堆排序是利用堆这个数据结构对数据进行排序,堆的特点是可以在构建完毕后以O(1)的时间找到最大或最小值。堆有很多种实现,最简单也是最常见的实现就是二项堆,其类似一个完全二叉树,不过是以数组形式呈现的,这时下标呈现一个规律,对于一个下标i的元素
- 其父节点的下标:
i/2-1 - 其左子节点的下标:
i*2+1 - 其右子节点的下标:
i*2+2
如果是升序排序,就构建大顶堆,反之构建小顶堆。
这里以升序为例,父节点与子节点进行比较,如果比子节点小就交换双方位置,交换后继续向下比较,直到遇到第一个比父节点更小的子节点,或者没有子节点了才停止,这个过程被称为下沉。对于一个切片而言,它的最后一个子树的根节点位置位于len(s)/2 -1,逆序遍历每一个子树根节点,对其进行下沉操作。在构建完毕后,此时堆顶的元素一定的最大的那一个,将其与切片中最后一个元素交换,然后再次对堆顶元素进行下沉操作,此时下沉范围不包括最后一个元素,因为已经确定了它是最大值。第二次下沉可以确认堆顶的元素是第二大的,将其与在切片的倒数第二下标的元素交换,然后下沉范围减一,继续第三次下沉,如此循环往复,每次下沉都能找到第k大的元素,最终整个切片都会有序。
func down[T any](s []T, l, r int, less func(a, b T) bool) {
for ls := l<<1 + 1; ls < r; ls = l<<1 + 1 {
rs := ls + 1
if rs < r && !less(s[rs], s[ls]) {
ls = rs
}
if less(s[ls], s[l]) {
break
}
s[ls], s[l] = s[l], s[ls]
l = ls
}
}
func HeapSort[T any](s []T, less func(a, b T) bool) {
// 构建大顶堆
for i := len(s)>>1 - 1; i >= 0; i-- {
down(s, i, len(s), less)
}
// 交换堆顶元素,不断缩小范围并对堆顶元素进行下沉
for i := len(s) - 1; i > 0; i-- {
s[0], s[i] = s[i], s[0]
down(s, 0, i, less)
}
}
时间复杂度:O(nlogn)
堆排序总共分为两步,第一步构建堆,由于是自底向上构建,如果一个高度为h的子树已经是堆了,那么高度为h+1的子树进行调整的话最多也只需要h步,构建堆的过程的时间复杂度可以是O(n),详细证明过程可以看:Build Binary heap - Wikipedia。在下沉的过程中,对于一个高度为h的完全二叉树而言,最多需要比较h-1次,而高度h就等于log2(n+1),总共下沉n-1次,其时间复杂度就近似为O(nlogn),并且不管在任何情况都是O(nlogn),不会受到数据的影响。
空间复杂度:O(1)
过程中没有用到任何的额外辅助空间
稳定性:否
在排序过程中,需要不断的将堆顶元素放交换到数组末尾,这一过程会破掉坏相等元素的相对位置。
性能测试
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkHeapSort/100-16 462600 2688 ns/op 0 B/op 0 allocs/op
BenchmarkHeapSort/1000-16 6410 167627 ns/op 0 B/op 0 allocs/op
BenchmarkHeapSort/10000-16 93 11975123 ns/op 0 B/op 0 allocs/op
BenchmarkHeapSort/100000-16 1 1136002700 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 16.270s
可以看到的是,在10w数据量的情况下,堆排序只需要1秒多一点。
归并排序
归并排序是分治思想的一个体现,1945年由约翰.冯.诺依曼首次提出。它的思路理解起来非常简单,看一个例子,现有如下数据
4 1 5 8 0 6 2 10
首先是分隔操作,将其分成两份
4 1 5 8 || 0 6 2 10
在两份的基础之上对半分
4 1 || 5 8 || 0 6 || 2 10
此时已经没法再分了,可以直接调整每一份内的顺序,由于只有两个数,只需要简单交换下,现在每一小份的数据内部都是有序的
1 4 || 5 8 || 0 6 || 2 10
接下来就是合并操作,先将其合并为2份,在合并的过程中,可以创建一个临时数组来保存结果,比如合并 0 6 || 2 10,第一步0比2小,所以先写入0
0
第二步,6比2大,所以写入2
0 2
第三步6比10小,所以写入6,最后写入10。
0 2 6 10
由于每小份内部都是有序的,在合并的时候只需要依次比较元素就可以得到更大的有序的部分,合并成两份数据如下
1 4 5 8 || 0 2 6 10
最终延续之前的操作,将其合并为一份,就可以得到排序后的数组。这个过程就是分治的过程,一整个数组不好排序,就将其分为更小的数组,直到不能再分,排序好后再不断合并为更大的有序数组,直到完成排序。这种方式天然适合递归来实现,当然也可以使用迭代来实现,只不过后者要自行模拟栈的行为,较为麻烦。
在递归方法中,分治是自顶向下的,仅当合并时才会用到临时数组用于写入数据,为了避免多次内存分配而影响性能,可以在排序开始前就分配好一个等大的临时数组。
func MergeSort[T any](s []T, less func(a, b T) bool) {
t := make([]T, len(s))
divide(s, t, 0, len(s)-1, less)
}
func divide[T any](s []T, t []T, l, r int, less func(a, b T) bool) {
if l >= r {
return
}
// 对半分
m := l + (r-l)>>1
// 分治左边
divide(s, t, l, m, less)
// 分治右边
divide(s, t, m+1, r, less)
// 合并两部分
merge(s, t, l, r, m, less)
}
func merge[T any](s []T, t []T, l, r, m int, less func(a, b T) bool) {
// 左右两个指针指向左右两个部分
li, ri := l, m+1
i := l
// 写入临时数组
for ; li <= m && ri <= r; i++ {
if less(s[li], s[ri]) {
t[i] = s[li]
li++
} else {
t[i] = s[ri]
ri++
}
}
// 还有左半边还有剩余元素就直接添加进去
for ; li <= m; i, li = i+1, li+1 {
t[i] = s[li]
}
// 右半边还有剩余元素也直接添加进去
for ; ri <= r; i, ri = i+1, ri+1 {
t[i] = s[ri]
}
// 正常写完后i指针是越界的,修正一下
i--
// 写回原数组
for ; i >= l; i-- {
s[i] = t[i]
}
}
在迭代方法中,不再需要逐个对半分,可以截取数组的部分直接进行合并,一开始两个两个合并,然后是四个,再然后是八个,十六个,这种方式是自底向上的。
func MergeSortI[T any](s []T, less func(a, b T) bool) {
t := make([]T, len(s))
// 步长,表示每一次截取多少个元素
var step int
for step = 1; step < len(s); step <<= 1 {
for i := 0; i < len(s); i += step << 1 {
l := i
m := min(l+step, len(s))
r := min(l+step+step, len(s))
// 合并数据,与之前一样
li, ri, k := l, m, l
for li < m && ri < r {
if less(s[li], s[ri]) {
t[k] = s[li]
li++
} else {
t[k] = s[ri]
ri++
}
k++
}
for ; li < m; k++ {
t[k] = s[li]
li++
}
for ; ri < r; k++ {
t[k] = s[ri]
ri++
}
}
// 将临时数组中的内容写入原数组用于准备下一轮合并
for i := 0; i < len(t); i++ {
s[i] = t[i]
}
}
}
递归的优点就是简单易懂,如果数据过大,可能会爆栈,而迭代的优点就是可以避免递归栈空间的开销,是真正意义上的O(n)空间,建议使用迭代法。
时间复杂度:O(nlogn)
拿迭代法举例分析,最外层循环每次都会乘2,可以确定是log2^n次,内层循环每次移动一个步长,然后在遍历步长范围内的元素,内循环总的遍历次数就是n次,内外总的时间复杂度就是O(nlogn)。归并排序和堆排序一样,不受数据的影响,始终都是O(nlogn)。
空间复杂度:O(n)
用到了一个临时数组来保存每一轮合并结果
稳定性:是
性能测试
下面是迭代和递归法两个一起测试的结果
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkMergeSort/100-16 483931 2915 ns/op 896 B/op 1 allocs/op
BenchmarkMergeSort/1000-16 22893 48469 ns/op 8192 B/op 1 allocs/op
BenchmarkMergeSort/10000-16 1533 749286 ns/op 81920 B/op 1 allocs/op
BenchmarkMergeSort/100000-16 135 8780795 ns/op 802819 B/op 1 allocs/op
BenchmarkMergeSortI/100-16 453235 2309 ns/op 896 B/op 1 allocs/op
BenchmarkMergeSortI/1000-16 25916 47443 ns/op 8192 B/op 1 allocs/op
BenchmarkMergeSortI/10000-16 1758 661138 ns/op 81920 B/op 1 allocs/op
BenchmarkMergeSortI/100000-16 154 7438036 ns/op 802817 B/op 1 allocs/op
PASS
ok sorts 60.562s
从时间效率上来看,迭代法总体是要优于递归法的,大概提升了10%-25%左右的时间效率。
快速排序
快速排序,又称分区交换排序,也用到了分治的思想,由英国计算机科学家东尼.霍尔在1959年提出。它的平均时间复杂度是O(nlogn),最差是O(n^2),尽管如此,在对随机数据的排序效果上,尤其是大量的随机数据,其时间效率的表现比归并排序和堆排序更好一些。
下面介绍一下快排的实现思路:假设有如下数据且是升序排序,总共有10个数字,快排的思路中也需要分治,不过它的方法不会像归并排序一样直接对半分,而是会选取一个基准值,将数组划分成两部分,左半边的部分都比这个基准值小,右半边的部分都比这个基准值大,具体的划分思路如下。
5 8 6 3 2 0 7 9 11 30
这里为了简单演示,选择5作为基准值,然后有左右两端两个指针指向最左和最右,左指针从左往右扫描,遇到比基准值大的元素停下来,右指针从右往左扫描,遇到比基准值小的元素停下来,下面用i表示左指针,j表示右指针。右边先开始扫描,遇到比基准值小的元素就停下,j停在了0所在的位置。
pivot: 5
5 8 6 3 2 0 7 9 11 30
i j
将j所指向的元素的值赋给i所指向的元素
pivot: 5
0 8 6 3 2 0 7 9 11 30
i j
然后左边开始扫描,遇到比基准值大的元素就停下,然后将i所指向元素的值赋给j所指向的元素
pivot: 5
0 8 6 3 2 8 7 9 11 30
i j
再然后j继续从右边开始扫描,遇到2停下,将其赋值给i所指向的元素,如此循环往复,直到两指针相遇
pivot: 5
0 2 6 3 2 8 7 9 11 30
i j
pivot: 5
0 2 6 3 6 8 7 9 11 30
i j
pivot: 5
0 2 3 3 6 8 7 9 11 30
i j
pivot: 5
0 2 3 3 6 8 7 9 11 30
i
j
相遇过后,此时i和j的位置,就是基准值在这个数组中排序后对应的位置,将基准值赋值到相遇位置上的元素
pivot: 5
0 2 3 5 6 8 7 9 11 30
i
j
此时可以发现,基准值5右边的所有数字都大于5,左边的数字全都小于5 ,说明在升序排序的情况下,数字5的下标就位于下标3,至此数字5的位置确定了,每一轮扫描都可以确定一个数字在数组中排序后的位置,接下来就是将数组分为两部分,0-2和4-9,再次对子数组进行相同的操作,直到不可再分。
另一点需要注意的是,如果基准值的选取默认选择在最左边的元素,那么在扫描的时候就需要右边先开始。如果从左边开始,那么左指针i扫描结束后会覆盖j所指向的值,但此处j指向的是最右边的值,把它覆盖过后这个值就丢失了。看下面一个例子,当第一次左指针i扫描完成后两个指针分别指向7和10
pivot: 5
5 2 4 1 3 7 8 9 10
i j
此时i会将7赋值给j所指向的元素,也就是将10覆盖为7
pivot: 5
5 2 4 1 3 7 8 9 7
i j
然后问题就出现了,10这个数字就不见了,当从右边先开始时,j所覆盖的第一个元素一定是最左边的基准值,因为基准值是单独记录的,所以不存在丢失的问题。同理,基准值取最右边的元素时,就需要左指针先动。考虑一种情况,如果基准值恰好是所有数字中最小的,就像下面的数据一样。
pivot: 1
1 2 3 4 5 6
由于总是右指针先开始,且基准值已经是最小的了,右指针会移动到1与左指针相遇然后停下,然后子数组被分成了[0,-1]和[1,5],只产生了一个有效的子数组,后面的每一次递归都是这种情况,第一层递归比较n-1次,第二层递归比较n-2次,第三层比较n-3次,总共会产生n-1次而不是log2n次递归调用,这样一来它的时间复杂度实际上就变成了O(n2)。
上面介绍的这个分区方法叫霍尔分区法,在其它教材比如《算法导论》以及英文wiki中介绍的一般是洛穆托分区法,它的代码实现更简单,比较适合用作教学。它的思路可以参考下面这个例子,选取基准值取最右边的元素5,然后有ij两个分别指针指向-1,0,它们的移动方向都是从左到右,并非左右双向指针。
pivot: 5
8 0 1 7 2 4 6 5
i j
j先开始扫描,遇到比基准值小的元素停下来,然后i向后移动一位,再交换ij所指向的元素,如此循环往复,直到j移动到最右边
pivot: 5
0 8 1 7 2 4 6 5
i j
pivot: 5
0 1 8 7 2 4 6 5
i j
pivot: 5
0 1 8 7 2 4 6 5
i j
pivot: 5
0 1 2 7 8 4 6 5
i j
pivot: 5
0 1 2 4 8 7 6 5
i j
pivot: 5
0 1 2 4 8 7 6 5
i j
扫描结束后,i此时指向的是最后一个小于基准值的数字,所以将i向后移动一位指向8
pivot: 5
0 1 2 4 8 7 6 5
i j
然后i,j指向的元素互换
pivot: 5
0 1 2 4 5 7 6 8
i j
此时基准值就被放到了正确的位置上来了,洛穆托分区法跟冒泡很相似,只不过它不会像冒泡一样逐个交换,而是跳跃式的,在最坏情况下,洛穆托分区法的时间复杂度也是O(n^2)。假设升序排序且洛穆托分区法基准值取的是左边,那么两个指针就要从右往左移,比较规则也要从小于换成大于。
代码实现
func QuickSortHoare[T any](s []T, less func(a, b T) bool) {
partitionHoare1(s, 0, len(s)-1, less)
}
func partitionHoare[T any](s []T, l, r int, less func(a, b T) bool) {
if l >= r {
return
}
// 记录基准值
pivot := s[l]
// 左右两个指针
i, j := l, r
for i < j {
// 右指针先动
for i < j && !less(s[j], pivot) {
j--
}
// 覆盖i所指向的值
s[i] = s[j]
// 左指针后动
for i < j && less(s[i], pivot) {
i++
}
// 覆盖j所指向的值
s[j] = s[i]
}
// 基准值归位
s[i] = pivot
partitionHoare(s, l, i-1, less)
partitionHoare(s, i+1, r, less)
}
func QuickSortLomuto[T any](s []T, less func(a, b T) bool) {
partitionLomuto(s, 0, len(s)-1, less)
}
func partitionLomuto[T any](s []T, l, r int, less func(a, b T) bool) {
if l >= r {
return
}
pivot := s[r]
// i初始位置指向-1
i := l - 1
// j指针不断向右移动
for j := l; j < r; j++ {
// 如果遇到小于基准值的元素,就移动i并交换它们的值
if less(s[j], pivot) {
i++
s[i], s[j] = s[j], s[i]
}
}
// 此时i指向的是最后一个小于基准值的元素
// 向后移动一位就是基准值的正确位置
i++
s[i], s[r] = s[r], s[i]
// 继续划分子数组
partitionLomuto(s, l, i-1, less)
partitionLomuto(s, i+1, r, less)
}
时间复杂度:O(nlogn)
每一趟扫描的时间复杂度是O(n),总共扫描log2^n次,所以总的时间复杂度是O(nlogn)。
空间复杂度:O(logn)
它在代码方面确实没有额外的空间,但在有些书籍中会将递归的栈空间也算入空间复杂度中,也就是O(logn),在上面介绍的最坏的情况下,它的空间复杂度可以达到O(n)。
性能测试
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkQuickSortHoare/100-16 837140 2484 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortHoare/1000-16 26656 47014 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortHoare/10000-16 888 1344127 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortHoare/100000-16 13 84603315 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortLomuto/100-16 650293 2199 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortLomuto/1000-16 33241 38348 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortLomuto/10000-16 900 1318429 ns/op 0 B/op 0 allocs/op
BenchmarkQuickSortLomuto/100000-16 13 85330962 ns/op 0 B/op 0 allocs/op
PASS
ok sorts 85.051s
两种分区法并没有特别明显的性能差距,但理论上来讲,洛穆托分区法的交换次数是是霍尔分区法的三倍(证明过程可以前往hoare vs lomuto了解细节)。
优化
上面的快排实现中,在10w数据量的情况下要88ms,同样情况下堆排序和归并排序只需要其十分之一的耗时,显然如此简单的快排实现是不足以应用到实际使用中的,必须对其进行优化。
优化点1
基准值如果是数组中的中位数,就可以做到较为均匀的划分子数组,避免出现取到最小最大值作为基准值的情况,但是取中位数是需要耗费额外的性能,常见的做法是将数组中左右端点和中间位置的三值间的中值作为基准值。
func threeMid[T any](s []T, l, r int, less func(a, b T) bool) int {
m := l + (r-l)>>1
// 将三个数中最大的放到r位置上
if less(s[r], s[l]) {
s[l], s[r] = s[r], s[l]
}
if less(s[r], s[m]) {
s[m], s[r] = s[r], s[m]
}
// 然后中值就在l,m两者之间
if less(s[l], s[m]) {
return m
}
return l
}
还有另一个方法就是随机选取。
优化点2
对于小数组而言,没有必要再用快排继续进行分区递归了,可以使用其它更为简单排序算法来代替,例如C++STL中的排序会在长度小于16时采用插入排序,因为插入排序对于小规模数据比冒泡和选择都更快,并且实现也很简单,转换的临界点也一般在5-16之间。
优化点3
如果含有大量的重复元素,时间复杂度仍然可能会恶化成平方级别。优化方法是使用三路快排,其思想是在单趟排序时将数组划分为三个部分,左边是小于基准值的部分,中间是等于基准值的部分,右边是大于基准值的部分,在后续的排序中,我们只需要处理小于和大于的部分,中间的可以完全不用管,三路快排对于处理有大量重复元素的数组很有效。
func sortArray(nums []int) []int {
partition(nums, 0, len(nums)-1)
return nums
}
func partition(nums []int, l, r int) {
if l >= r {
return
}
// 随机挑选基准值
n := rand.Intn(r-l+1) + l
nums[l], nums[n] = nums[n], nums[l]
pivot := nums[l]
lt := l
gt := r + 1
// [lt+1..i] == v
i := l + 1
for i < gt {
if nums[i] < pivot {
nums[i], nums[lt+1] = nums[lt+1], nums[i]
i++
lt++
} else if nums[i] > pivot {
// 交换后的数字不一定就小于基准值,所以不移动i,需要下个循环再次判断
nums[i], nums[gt-1] = nums[gt-1], nums[i]
gt--
} else {
i++
}
}
// lt是等于基准值数组的左边界,此时再和基准值进行交换
nums[lt], nums[l] = nums[l], nums[lt]
// 继续不断分支排序
partition(nums, l, lt-1)
partition(nums, gt, r)
}
[l, lt-1]表示小于基准值的范围,[gt, r]表示大于基准值的范围,[lt, i]就是等于基准值的范围。举一个例子,如下图
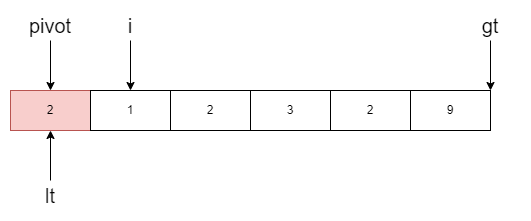
我们的任务是将小于基准值的移动到数组左边,大于基准值的移动到右边,所以i不断遍历数组。当i指向的元素小于基准值时,右移lt一位
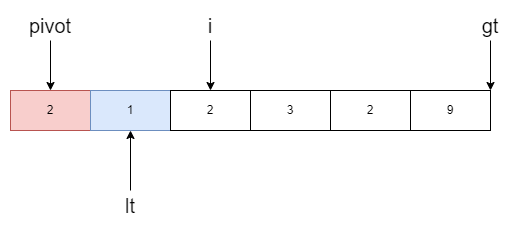
此时i指向元素2,等于基准值于是跳过
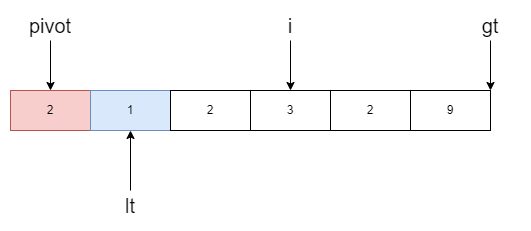
现在i指向的值是3,大于基准值,gt指针左移并和i所指的元素进行交换。
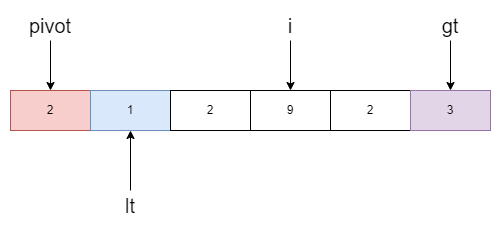
但交换后的值仍然大于基准值于是继续移动gt指针然后再交换。
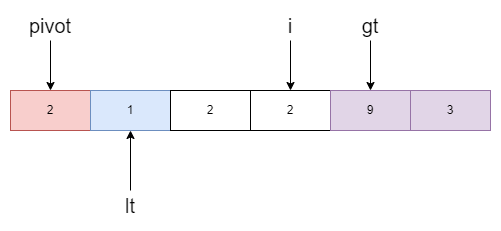
此时的i指向了2,与基准值相同则继续移动,直到等于gt。最后再将基准值归位,即lt与pivot交换位置。
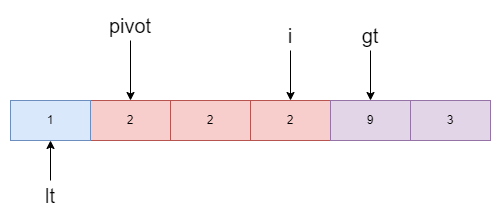
至此,区间的划分已经完毕,接下来在进行递归时我们只需要关注左右两个区间即可,中间的就可以忽略掉,这样就起到了优化大量重复元素d
计数排序
计数排序是一种线性时间的排序算法,并且是非比较排序,虽然它可以达到线性时间复杂度,但对使用的数据有一定的要求:数据之间的差值不能有太大,并且会使用额外的辅助空间。它的实现思路如下,首先统计数据中的最小最大值,然后使用一个长度为max-min+1的数组来记录每一个数据的个数,对于计数数组,下标i就等于数据的值,这样一来通过计数数组,天然的就能将其排序,然后反向遍历计数数组根据数量填充原数组。由于数据的限制,该排序方法不太好通过泛型来实现。
func CountSort(s []int) {
var minE, maxE int
for _, e := range s {
if e < minE {
minE = e
}
if e > maxE {
maxE = e
}
}
counts := make([]int, maxE-minE+1)
// 这里是正向的读取数据
// 为保证稳定性后面排序的时候就要反向的存放
// 怎么读的就怎么存
for _, e := range s {
counts[e-minE]++
}
// 逆序写
for i, k := len(counts)-1, len(s)-1; i >= 0; i-- {
for j := counts[i]; j > 0; j-- {
s[k] = minE + i
k--
}
}
}
时间复杂度:O(n+k)
寻找最大最小值时花费O(n),k是最大值和最小值的差值,在计数后写入原数组时,至少会循环k次,所以时间复杂度O(n+k)。当k值远大于O(nlogn)时,说明就不适合使用计数排序来对数据进行排序。
空间复杂度:O(k)
这里用到了counts数组来存放数量信息,花费空间O(k)。我看到网上很多其它实现都会用一个临时数组来存储结果再复制到目标数组中去,这样一来空间复杂度就变成了O(n+k),不太明白这样做的意义是什么。
稳定性:是
正序读,逆序写保证了相等数据的相对位置。
性能测试
计数排序是用在特定场景的排序方法,不适合随机数据排序,下面的测试用例中的生成数据中的最大差值在1w以内。
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkCountSort/100-16 100839 11764 ns/op 81921 B/op 1 allocs/op
BenchmarkCountSort/1000-16 62029 19060 ns/op 81921 B/op 1 allocs/op
BenchmarkCountSort/10000-16 15981 73497 ns/op 81942 B/op 1 allocs/op
BenchmarkCountSort/100000-16 4191 266531 ns/op 82900 B/op 1 allocs/op
PASS
ok sorts 16.788s
可以看到的是即便是数据量来到了10w级别,也没有出现较大的增幅。
基数排序
基数排序同计数排序一样,是非比较排序,同样只适用于特殊场景,不适合普遍的随机数据排序。它的排序思路是根据数据的位数来决定,可以从高位到低位,也可以从低位到高位。这里以以低位到高位举例,比较好理解。现有如下数据,低位数据自动补零方便理解。
152 003 012 948
首先将其按照个位的大小排序,得到下面的序列
152 012 003 948
在其基础之上根据十位排序得到下面的序列
003 012 948 152
在其基础知识根据百位排序
003 012 152 948
最终得到有序的数组,基数排序的思路非常简单明了容易理解,代码实现如下
func RadixSort(s []int) {
maxV := slices.Max(s)
// 最大位数
bit := 0
for maxV > 0 {
maxV /= 10
bit++
}
// 0-9 10个数字
count := make([]int, 10)
// 临时数组,用来保存每一轮的排序结果
temp := make([]int, len(s))
radix := 1
// 最大数有多少位,就遍历多少次
for i := 0; i < bit; i++ {
clear(count)
for _, e := range s {
count[(e/radix)%10]++
}
// 累加后count数组每一个元素记录着由(s[i]/radix)%10计算得到的最后一个元素位置
for i := 1; i < len(count); i++ {
count[i] += count[i-1]
}
// 正序读逆序写,保证稳定性
for i := len(s) - 1; i >= 0; i-- {
temp[count[(s[i]/radix)%10]-1] = s[i]
// 下一个被分配此位置的元素
count[(s[i]/radix)%10]--
}
copy(s, temp)
// 进一位
radix *= 10
}
}
可以看到的是在过程中,每一轮的排序方式其实就是计数排序变种,每一个位上的差值最大也就只有9,所以count数组长度也就是固定的10。计数分配好后,因为在这里分配的下标不代表实际的值,所以要累加每一个计数的值,这样就能得到它们排序后的位置。后面就是将其写入临时数组,再复制到原数组中。
时间复杂度:O(kn)
k的最大值的位数,也决定了外层循环的次数,每一次外循环花费的时间是O(n),总共就是O(nk)。
空间复杂度:O(n+k)
用到了一个长度为n的临时数组用于存放每轮排序结果,和一个计数数组。
稳定性:是
跟计数一样,正序读,逆序写保证了相等数据的相对位置。
性能测试
goos: windows
goarch: amd64
pkg: sorts
cpu: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
BenchmarkRadixSort/100-16 155721 7971 ns/op 896 B/op 1 allocs/op
BenchmarkRadixSort/1000-16 15081 78742 ns/op 8192 B/op 1 allocs/op
BenchmarkRadixSort/10000-16 1501 777792 ns/op 81920 B/op 1 allocs/op
BenchmarkRadixSort/100000-16 150 7913457 ns/op 802819 B/op 1 allocs/op
PASS
ok sorts 15.333s
这里生成的随机数据只包含正整数,10w数据量的情况下只需要7ms,指的是注意的是,基数的选择不止是10进制还可以是十六进制,八进制,二机制,每个进制的基数范围不同。那么为什么它的性能相当优秀但使用没有快排广泛,思考下总共有几点:
- 不太好抽象,适用面窄,比如这个基数排序的例子我都是用int来写的,很难用泛型实现,如果是结构体类型,那么它的特征值可能是浮点数,字符串,或者是负数,甚至是复数,这些类型很对基数进行分解,也就谈不上排序。
- 第二点就是额外的O(n)空间。
